UnityのNative Pluginを作ってC++のコードやライブラリを使う

Unity 開発

概要

UnityといえばC#で開発するのが基本ですが、Native Pluginという機能を使えば、他の言語 (C++など) で書かれたコードを呼び出すことができます。

今回はじめてNative Pluginを作ってみたので、調べたことなどをメモしておきたいと思います。


f:id:yuki-koyama:20151118191833p:plain
C++のライブラリ (Eigenとlibigl) を用いてUnity上でメッシュのガウス曲率を可視化した例

背景と動機

普段はC++でコンピュータグラフィクス関連の研究をしています（プロダクトの開発は行なっていません）。私がC++を使う主な理由は

  • 過去に自分で書いたコードを使いまわしたいから
  • 優秀な数学演算のライブラリや高度なジオメトリ処理のライブラリを使えるから
  • 高速化がしやすいから

などです。一方でUnityを使うこともあります。私がUnityを使う際の主な理由は

  • 優秀なリアルタイムレンダリングが予め用意されているから
  • Unity Asset Storeから優秀なモデルデータを入手できるから
  • インタラクションの実装が (C++に比べて) 容易だから

などです。

つまり、技術自体を作り込むにはC++が便利だけど、技術デモを作り込むにはUnityが便利なわけです。このトレードオフを解決する手段として、C++で開発した技術をUnityのNative Pluginとして呼び出すという方法を試してみることにしました。

環境

今回は複数アーキテクチャへのデプロイについては考えません。

C言語でインタフェースを作る

C#からC++で作ったNative Plugin (動的ライブラリ) の機能を呼ぶには、C言語の関数でやりとりするようです。例えばC++側では以下のようなC言語の関数を定義しておきます：

extern "C" {
    void* InstantiateMesh(const int* triangles, const double* vertices, int numberOfTriangles, int numberOfVertices);
    void DeleteMesh(void* mesh);
}

なおextern "C"という宣言はC++のName Manglingを回避するために必須なのだそうです。上記の関数は、C#側で以下のように宣言することで使用可能になるようです：

[DllImport ("PluginName")]
private static extern IntPtr InstantiateMesh(IntPtr triangles, IntPtr vertices, int numberOfTriangles, int numberOfVertices);

[DllImport ("PluginName")]
private static extern void DeleteMesh(IntPtr mesh);

intやdoubleは両言語共通で使えるようです。IntPtrとはポインタのことだそうです。

Xcodeでバンドルをビルドする (Mac OS X)

上記のサイトに従ってバンドル (.bundle) を作成し、UnityプロジェクトのAsset以下の適切な場所に配置します。

この際の注意点は、target architecturesの設定です。Unity 4のエディタは32-bitで動いているようなので、32-bit用のバンドルを作成する必要があります。その場合はi386を指定します。また、Unity 5は64-bitにも対応しているそうです。その場合はx86_64を指定します。これは意外に面倒な問題です。

ここで一番良いと思われる方法は、公式マニュアルでも言及されている通り、Mac OS Xについてはいつでもユニバーサルバイナリを作ることです。ユニバーサルバイナリとは複数のアーキテクチャで使えるバイナリです。Xcodeでもそのような選択肢が用意されています。


f:id:yuki-koyama:20151118192017p:plain
Xcode上でユニバーサルバイナリを指定

もう一つ注意点としては、既存のビルド済みスタティックライブラリを用いてユニバーサルバイナリをビルドするには、既存のライブラリもまたユニバーサルバイナリとしてビルドされている必要があります。例えばHomebrewで

$ brew install boost

などのコマンドでライブラリ (ここではboost) をいれている場合は、普通ユニバーサルバイナリとしてビルドしてくれていません。この問題を解決するには

$ brew reinstall boost --universal

とすることでユニバーサルバイナリとしてビルドしなおしてくれるようです。

なお

$ lipo -info (ライブラリへのパス)

などとすると既存のライブラリがどのアーキテクチャ向けにビルドされているか確認することができます。

ただしHomebrewのオプションを指定する方法は（なぜか）いつでもうまくいくわけではないようで、いくつかのライブラリについてはユニバーサルバイナリを作ってくれないようです。自分の場合はCGALというジオメトリ処理用のライブラリをHomebrewでいれようとしても、うまくユニバーサルバイナリを作ってくれませんでした。そこでHomebrewを諦めてCMakeでCGALをビルドすることにしました。CMakeでは

CMAKE_OSX_ARCHITECTURES=x86_64;i386

と指定するとユニバーサルバイナリを作ってくれます。

C#からC++へ配列を渡す

配列のやりとりは基本的にはポインタのやりとりになりますが、C#にはmanagedとかunmanagedとかいう概念があるそうで（C#に疎いので知りませんでした）、ちょっと工夫が必要です。例えばint型の配列をC#からC++に渡すには以下のようにするようです：

int[] triangles = mesh.triangles;
IntPtr unmanagedTriangles = Marshal.AllocHGlobal(triangles.Length * sizeof(int));
Marshal.Copy(triangles, 0, unmanagedTriangles, triangles.Length);
// ここでunmanagedTrianglesを使ってC++の関数を呼ぶ
Marshal.FreeHGlobal(unmanagedTriangles);

このコードは手元では動きましたが、ググると色々な人が色々な方法を提示しているので、これが正解ではないかもしれません。

C++からC#へ配列を渡す

これもmanagedとかunmanagedとかいう概念を考慮する必要があるらしく、例えばdouble型の配列を受け取るには以下のようにすれば良いようです：

IntPtr tempPtr = IntPtr.Zero;
int arrayLength = 0;
SomeFunctionInNativePlugin(ref tempPtr, ref arrayLength);
double[] array = new double[arrayLength];
Marshal.Copy(tempPtr, array, 0, arrayLength);
// ここで何らかの手段でtempPtrが指すメモリ領域を解放する

ちなみにC++側で配列の実体をメモリ上に確保しているはずなので、あとで必ずC++側でメモリを解放する必要があります。

C++のクラスをC#で使う

上記のようなラッパーを書けばC#側からC++のクラスをインスタンス化したりメソッドを呼んだりできそうです。ただしこれはかなり面倒そうです。誰かラッパーを自動生成するスクリプト書いてください。

C++とC#で構造体をやりとりする

かなり面倒くさそうです。

余談：コンピュータグラフィクスの研究にどう使うか

コンピュータグラフィクスの要素技術研究に伴う開発では、もちろん研究内容によりますが、頻繁に仕様変更がおきたり、様々な実装の可能性を試行錯誤していく必要が生じます。そういった研究の初期段階では、C++とUnityを組み合わせた開発スタイルではラッパークラスなど本質的でないコードの変更が大量に発生するため、かなり効率が悪そうだと感じました。やはりC++でテスト用のレンダラを実装したりテストシーンを構築したりする方が良さそうです。技術の内容が完全に確定し、論文を書いたり人に見せるためのデモ用シーンを作ったりする段階になって初めてUnityと組み合わせるというのが現実的な選択肢だと思いました。

最後に

間違い・意見などありましたらご連絡いただけると幸いです。

*1:TwitterでUnity 4 Proを使っていると呟いたところ、複数人からUnity 5 (non Pro) に移行した方が良いと勧められました。Unity 4を使っている人は特別な理由がない限りいますぐUnity 5に移行した方が良さそうです。

論文読み: Position Based Fluids (SIGGRAPH '13) その２

論文 CG SIGGRAPH 2013 開発 習作 Unity

実装してみた

この記事は過去に書いた記事の続きです：

yuki-koyama.hatenablog.com

これまで流体シミュレーションを実装したことが一度もなかったため、一度ぐらいやってみようということで、最近流行りの Position-Based Fluids（のようなもの）の実装に挑戦してみました。

論文の読み直しと実装で合わせて４時間程度でした。もちろん論文の隅から隅まで理解して全てを実装したわけではなく、一番重要なアイデアの部分だけを実装しています。よく見ると挙動が怪しいので、どこか数式を間違えているのかもしれません。

本気でちゃんと作り込めば、以下のような流体シミュレーションがリアルタイムで動くはずです。

読んだ論文は以下の２つです。

Matthias Müller, David Charypar, and Markus Gross
Particle-based fluid simulation for interactive applications
SCA '03

Miles Macklin and Matthias Müller
Position based fluids
SIGGRAPH '13

論文の概要

背景１：Smoothed Particle Hydro-Dynamics (SPH) 法

ゲームなどで使われるリアルタイムの流体シミュレーションといえば SPH (Smoothed Particle Hydro-dynamics) に基づく手法が有名です。SPH という考え方自体は古くからあるのですが、2003 年に Muller らが SCA という会議で発表した論文をきっかけに、コンピュータグラフィクス分野で広く使われるようになりました。

SPH は簡単にいうと粒子間の影響を補間する手法です。

背景２：Position-Based Dynamics (PBD)

流体シミュレーションとは別の文脈で、同じく Muller らが 2006 年に提案した物理シミュレーションのための枠組みで PBD (Position-Based Dynamics) と呼ばれる手法があります。これは従来の陽的オイラー法よりも安定でかつ陰的オイラー法よりも高速な時間積分 (Verlet) を利用しており、NVIDIA PhysX, Maya, Houdini でも採用されています。

yuki-koyama.hatenablog.com

PBD は、物体の振る舞いを力を用いて表現するのではなく、位置に基づく制約として表現する枠組みになっています。

Position-Based Fluids

今回の対象となる Position-Based Fluids もまた同じく Muller らによって 2013 年に提案されました。Position-Based Fluids を多少乱暴にいうと「PBD の枠組みの中で動く SPH 法」という感じです（流体の専門家には怒られるかもしれません）。SPH 法ではナビエストークス方程式から粒子に働く力を表現していたのに対し、Position-Based Fluids では流体の非圧縮性を位置に基づく制約として表現することで粒子の振る舞いを決定します。

具体的には以下の制約を考えます。

\displaystyle{ C_i (\mathbf{p}_1, \ldots, \mathbf{p}_n) = \frac{\rho_i}{\rho_0} - 1 }

ここで i は粒子のインデックス、\mathbf{p}_i は i 番目の粒子の位置、\rho_i は i 番目の粒子周りの密度、\rho_0 はこの流体の通常の状態での密度です。できるだけ C_i=0 \:\:(i=1, \ldots, n) となるように粒子の位置を決定することで、流体の振る舞いを表現します。ここで、\rho_i を推定する部分で SPH のアイデアを用いています。

実装した感想

  • Unity はプロトタイピングにすごく便利。可視化の部分のコードを書かなくても Unity がやってくれる。
  • 近傍探索の高速化は必須。ナイーブな実装だと O(n^2) で効いてくるのですぐに計算が重くなってしまう。
  • GPU 化は必須。弾性体シミュレーションや剛体シミュレーションに比べ流体シミュレーションは自由度が大きくなりがちなため、すぐに計算が重くなってしまう。PBD や Position-Based Fluids は GPU-Friendly なので GPU 実装するべき。
  • 水面の復元を実装するのはすこし大変そう。特に論文では GPU 実装しているが、これは結構大変そう。
  • 本気で全てを実装すると数ヶ月はかかりそう。

最近の話題

Position-Based Fluids や SPH 法は次から次へと新しい論文が出てくるホットな分野です。いくつかピックアップして紹介します。

粘性に関する論文：

Tetsuya Takahashi, Yoshinori Dobashi, Issei Fujishiro, Tomoyuki Nishita, and Ming C. Lin.
Implicit Formulation for SPH-based Viscous Fluids
Eurographics 2015
Project page

複数の流体の扱いに関する論文：

Tao Yang, Jian Chang, Bo Ren, Ming C. Lin, Jian Jun Zhang and Shi-Min Hu.
Fast Multiple-Fluid Simulation Using Helmholtz Free Energy
SIGGRAPH Asia 2015.
Project page

対話型機械学習 (Interactive Machine Learning, IML) について

機械学習 HCI

普段は Computer Graphics や Human-Computer Interaction を勉強しているのですが、最近は機械学習も少し勉強しています。今回は Human-Computer Interaction とも関わりの深いトピックである「対話型機械学習 (Interactive Machine Learning, IML)」について簡単にまとめます。

参考文献

ある機械学習の専門家にこちらの記事をおすすめされました。

Saleema Amershi, Maya Cakmak, W. Bradley Knox, Todd Kulesza:
Power to the People: The Role of Humans in Interactive Machine Learning.
AI Magazine 35(4): 105-120 (2014)
PDF download

この文献は interactive machine learning のサーベイというよりは、この分野を知らない人のための教科書的な導入として書かれているようです。

Interactive Machine Learning とは

そもそも伝統的な機械学習は

[...] a powerful tool for transforming data into computational models that can drive user-facing applications.

です。つまり、データがあって、ユーザがいるわけですが、ここで問題となるのはこの "computational models" を構築する作業は肝心のユーザではなく別の "skilled practitioners" (データサイエンティスト？) が行うという点です。したがって、この "practitioners" は実際のユーザと打ち合わせをしながら、適切な特徴量選択やパラメタチューニングを反復的に行っていく必要がありました。


f:id:yuki-koyama:20151010140140p:plain
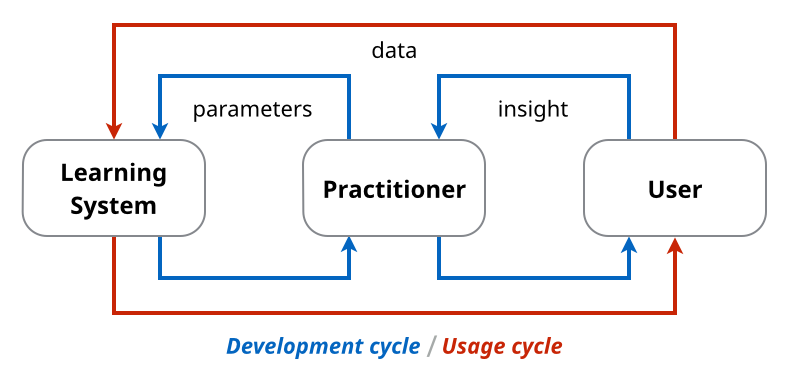
伝統的な機械学習ではユーザが直接モデル構築を行わないため学習と使用が乖離している。

伝統的な機械学習に対し、モデル構築の過程で直接ユーザと対話することで、より良いユーザエクスペリエンスやより効果的な学習機構を目指すものを interactive machine learning と呼ぶようです。これによって、例えば "practitioners" を挟む間接的なやり方よりも、直接学習と使用のサイクルを回すことができます。


f:id:yuki-koyama:20151010140144p:plain
Interactive Machine Learning ではユーザが直接モデル構築に関与する。

文献の中では、伝統的な機械学習と比較した際の interactive machine learning の特徴として、以下の三点が挙げられています。

  • モデルの更新がより rapid である（ユーザ入力に対し即座にモデルを更新する）
  • モデルの更新がより focused である（モデルの特定の側面だけが更新される）
  • モデルの更新がより incremental である（一回の更新の大きさが小さく、劇的に変わることがない）

これらの条件が満たされることによって、機械学習の専門家でないユーザでも "low-cost trial-and-error or focused experimentation with inputs and outputs" をすることができ、効果的になると述べられています。

事例：画像のセグメンテーションにおける Interactive Machine Learning

Human-computer interaction の文脈において interactive machine learning という言葉が初めて使われたのは以下の論文だそうです：

Jerry Alan Fails and Dan R. Olsen, Jr..
Interactive machine learning.
In Proc. IUI '03. (Best Paper Award)
PDF download

この研究は画像のセグメンテーション（ここでは前景と背景を分ける）において、ユーザが前景（または背景）のピクセル群をブラシストロークによって対話的にマークしていくことで classifier の学習を進めていくという手法が提案されています。

これはちょうど Adobe Photoshop CC 2015 などに搭載されている「クイック選択ツール」の挙動と似ていると思います：

また、この研究で行われたユーザスタディにおいて得られた重要な知見の一つとして、システムの挙動（その時点での classifier によって得られるセグメンテーションの可視化）に応じてユーザが挙動（どこを次にマークするか）を変えた、という点が挙げられます。具体的には、システムがセグメンテーションに失敗した部分をユーザが直す、ということが行われたそうです。この事実は、interactive machine learning では interaction design が学習の効果に大きく寄与するということを示唆していると考えられます。

Interactive Machine Learning に関する学会・会議など

Interactive machine learning の研究は主に CHI, UIST, IUI などの human-computer interaction に関する国際会議で発表されることが多いようです。これは、学習で用いられるモデルそのものよりも、interaction design における知見や human factor の扱いに関する知見が interactive machine learning においては大きな課題であるからだと思われます。

共分散行列を含む多次元のガウス関数の微分

数学 機械学習

目的：ガウス関数の微分

共分散行列 \mathbf{\Sigma} (バンド幅行列) を用いて表された多次元 (多変量) で異方性のガウス関数 (多変量正規分布) の微分 (勾配) を考えます。微分したいガウス関数の形は

\displaystyle{ \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) = \frac{1}{(2\pi)^{\frac{n}{2}}|\mathbf{\Sigma}|^{\frac{1}{2}}}\exp\left( - \frac{1}{2} (\mathbf{x - {\boldsymbol \mu}})^T \mathbf{\Sigma}^{-1} (\mathbf{x - {\boldsymbol \mu}})\right) }

だとします。ただし \mathbf{\Sigma} \in \mathbb{R}^{n \times n} は正値対称な共分散行列 (バンド幅行列) で、\mathbf{x}, {\boldsymbol \mu} \in \mathbb{R}^n です。これはPRMLなどの機械学習の参考書でも見られるガウス分布の表し方です。

共分散行列を \mathbf{\Sigma}、中心を {\boldsymbol \mu} とするような多次元のガウス関数 \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) のイメージ。

ちなみにバンド幅が \sigma \in \mathbb{R} によって表された \mu \in \mathbb{R} を中心とする 1 次元のガウス関数

\displaystyle{ \mathcal{N}(x; \mu, \sigma) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left(- \frac{(x - \mu)^2}{2\sigma^2} \right) }

の微分は

などでも紹介されている通り、

\displaystyle{ \frac{d}{dx}\mathcal{N}(x; \mu, \sigma) = - \frac{x - \mu}{\sqrt{2\pi}\sigma^3} \exp\left(- \frac{(x - \mu)^2}{2\sigma^2} \right) }

となります。今回はこれの n 次元への拡張、さらにバンド幅が等方性ではなく異方性のものを微分します。

準備：指数部にベクトル・行列が含まれるときのベクトルによる微分

\mathbf{x} を n \times 1 ベクトル、\mathbf{A} を n \times n 対称行列とするとき、

\displaystyle{ \frac{\partial}{\partial \mathbf{x}} \left( \mathbf{x}^T \mathbf{A} \mathbf{x} \right) = 2 \mathbf{A} \mathbf{x} }

が成り立ちます。この公式自体は様々な記事やウェブサイトで紹介されているので、ウェブ検索をかけるとすぐに見つかります。

この公式と合成関数の微分の公式 (Chain Rule) を用いることで、

\displaystyle{ \frac{\partial}{\partial \mathbf{x}} \left\{ \exp \left( - \frac{1}{2}\mathbf{x}^T \mathbf{A}\mathbf{x} \right) \right\} \\ = \frac{\partial y}{\partial \mathbf{x}} \cdot \frac{\partial}{\partial y} \exp(y) \:\:\: \left( y := - \frac{1}{2}\mathbf{x}^T\mathbf{A}\mathbf{x} \right) \\ = - \frac{1}{2} \cdot \frac{\partial}{\partial \mathbf{x}} \left( \mathbf{x}^T\mathbf{A}\mathbf{x} \right) \cdot \exp(y) \\ = - \frac{1}{2} \cdot 2 \mathbf{A} \mathbf{x} \cdot \exp \left( - \frac{1}{2}\mathbf{x}^T\mathbf{A}\mathbf{x} \right) \\ = - \exp \left( - \frac{1}{2} \mathbf{x}^T \mathbf{A} \mathbf{x} \right) \mathbf{A} \mathbf{x} }

という関係式を導くことができます。この式は

では公式として紹介されています。ちなみにベクトルによる微分の Chain Rule は

で証明が紹介されています。

導出：式変形と結果

上記で導いた関係式と再び合成関数の微分の公式 (Chain Rule) を用いると

\displaystyle{ \frac{\partial}{\partial \mathbf{x}} \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \\ = \frac{1}{(2\pi)^{\frac{n}{2}}|\mathbf{\Sigma}|^{\frac{1}{2}}} \cdot \frac{\partial}{\partial \mathbf{x}} \exp\left( - \frac{1}{2} (\mathbf{x - {\boldsymbol \mu}})^T \mathbf{\Sigma}^{-1} (\mathbf{x - {\boldsymbol \mu}})\right) \\ = \frac{1}{(2\pi)^{\frac{n}{2}}|\mathbf{\Sigma}|^{\frac{1}{2}}} \cdot \frac{\partial \mathbf{z}}{\partial \mathbf{x}} \cdot \frac{\partial}{\partial \mathbf{z}} \exp\left( - \frac{1}{2} \mathbf{z}^T \mathbf{\Sigma}^{-1} \mathbf{z} \right) \:\:\: \left( \mathbf{z} := \mathbf{x} - {\boldsymbol \mu} \right) \\ = \frac{1}{(2\pi)^{\frac{n}{2}}|\mathbf{\Sigma}|^{\frac{1}{2}}} \cdot \mathbf{I} \cdot \left\{ - \exp\left( - \frac{1}{2} \mathbf{z}^T \mathbf{\Sigma}^{-1} \mathbf{z} \right) \mathbf{\Sigma}^{-1} \mathbf{z} \right\} \\ = - \frac{1}{(2\pi)^{\frac{n}{2}}|\mathbf{\Sigma}|^{\frac{1}{2}}} \exp\left( - \frac{1}{2} (\mathbf{x} - {\boldsymbol \mu})^T \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right) \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \\ = - \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) }

が得られます。また、冒頭で紹介した 1 次元のガウス関数の微分の関係式
\displaystyle{ \frac{d}{dx}\mathcal{N}(x; \mu, \sigma) = - \frac{x - \mu}{\sqrt{2\pi}\sigma^3} \exp\left(- \frac{(x - \mu)^2}{2\sigma^2} \right) }

も、得られた式において \mathbf{\Sigma} を \sigma^2 で置き換え n=1 とすることで、確かに成り立っていることが分かります。

おまけ：二階微分（ヘッセ行列）

上記で得られた結果をさらに用いて、ガウス関数の ヘッセ行列 (Hessian Matrix) を求めます。

ベクトル \mathbf{x} を引数とするスカラー関数 f(\mathbf{x}) のヘッセ行列 \mathbf{H} は

で説明されている通り、

\displaystyle{ \mathbf{H} = \frac{\partial^2}{\partial \mathbf{x} \partial \mathbf{x}^T} f(\mathbf{x}) = \frac{\partial}{\partial \mathbf{x}} \left( \frac{\partial}{\partial \mathbf{x}} f(\mathbf{x}) \right)^T }

で計算されます。したがって、ガウス関数のヘッセ行列は
\displaystyle{ \mathbf{H} = \frac{\partial^2}{\partial \mathbf{x} \partial \mathbf{x}^T} \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \\ = \frac{\partial}{\partial \mathbf{x}} \left\{ \frac{\partial}{\partial \mathbf{x}} \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \right\}^T \\ = \frac{\partial}{\partial \mathbf{x}} \left\{ - \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right\}^T \\ = - \left\{ \frac{\partial}{\partial \mathbf{x}} \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \right\} \left( \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right)^T - \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \left\{ \frac{\partial}{\partial \mathbf{x}} \left( \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right)^T \right\} \\ = - \left( - \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right) \left( \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right)^T - \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \mathbf{\Sigma}^{-1} \\ = \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \left\{ \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) (\mathbf{x} - {\boldsymbol \mu})^T \mathbf{\Sigma}^{-1} - \mathbf{\Sigma}^{-1} \right\} }

となります。途中、(\mathbf{\Sigma}^{-1})^T = \mathbf{\Sigma}^{-1} が成り立つことと、ベクトルによる微分に関する積の微分の関係式を用いました。一階微分を計算したときと同様に、\mathbf{\Sigma} を \sigma^2 で置き換え n=1 とすることで

で示されている結果などと矛盾しないことが分かります。

最後に

この記事には間違いがある可能性があります。ここに書かれている数式を用いる場合には必ず自身で再計算して確認してからにしてください。また、もし間違いを見つけた場合には教えてください。