RBF 補間 (Radial Basis Function Interpolation) の概要と実装

はじめに

RBF 補間とは

RBF 補間とは、RBF (放射基底関数, radial basis function) を用いて入力となる散布データ (scattered data) の値を補間することです。または、与えられた散布データを元に非線形な関数をフィッティング (または近似) することだと考えることもできます。

どういうときに使えるか

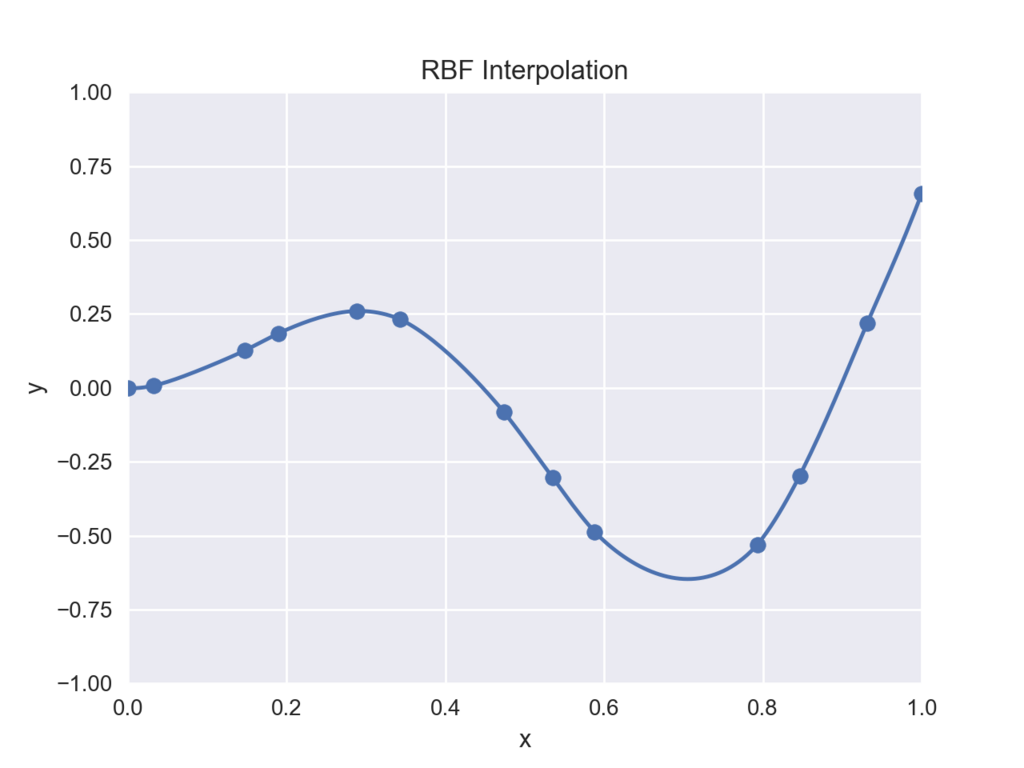
下図のように、 $N$ 個の点列 $(x_1, y_1), \ldots , (x_N, y_N)$ が与えられ、それらの点を通るような滑らかな関数 $f$ を求めたいときに、RBF 補間が使えます。

f:id:yuki-koyama:20180312163612p:plain

また、より高次元 ( $n$ 次元とします) の空間における補間も可能です。この場合は $N$ 個の点列 $(\mathbf{x}_1, y_1), \ldots , (\mathbf{x}_N, y_N)$ が与えられたときに関数 $f: \mathbb{R}^n \rightarrow \mathbb{R}$ を求めることになります。

どういう特徴があるか

RBF 補間はノンパラメトリックなフィッティングの一種です。
与えられた点列を必ず通るような関数を求めることができます。
ノイズが多く密度の高いデータに対しては過学習 (over-fitting) が起きることがあります。
一度事前計算さえすれば、補間値の評価は (比較的) 高速に行うことができます。

RBF ネットワーク

この記事で紹介する内容は、機械学習などの分野では RBF ネットワークと紹介されることも多いようです。私の専門分野 (Computer Graphics) では散布データを補間する目的で使われるため RBF 補間と呼ぶことが多いようです。*1

RBF 補間の考え方

RBF とは

RBF とは、基本的には「その値が原点からの距離にのみ依存する実数値関数」のことを指し、普通 $\phi$ で表します。

$\displaystyle{ \phi(\mathbf{x}) = \left \| \mathbf{x} \right \| \\ \phi(\mathbf{x}) = \exp ( - \beta \left \| \mathbf{x} \right \| ) \:\: (\beta > 0) }$

などは代表的な RBF です。

また、「その値が RBF Center $\mathbf{c}$ からの距離のみに依存する実数値関数」も含めて RBF と呼ぶことがあります。この場合は入力 $\mathbf{x}$ に対して $\phi(\mathbf{x}, \mathbf{c}) = \phi(\left \| \mathbf{x} - \mathbf{c} \right \|)$ となります。

関数の表現

RBF 補間では、ある重み $\mathbf{w} = (w_1, \ldots , w_N)$ を用いて、関数 $f$ を

$\displaystyle{ f(\mathbf{x}) = \sum_i^N w_i \phi(\mathbf{x}, \mathbf{x}_i) }$

と表します。つまり、RBF の重み付き線形和です。あとは与えられたデータに対してこの重みを予め上手く見つけておけば良いということになります。

重みの決め方

$j$ 番目の入力データ $(\mathbf{x}_j, y_j)$ に関して、重み $\mathbf{w}$ が満たすべき条件式として次のような式を考えます。

$\displaystyle{ y_j = \sum_i^N w_i \phi(\mathbf{x}_j, \mathbf{x}_i) }$

つまり、得られる関数 $f$ が点 $(\mathbf{x}_j, y_j)$ を通るという条件です。これを $j=1, \ldots , N$ の全てについて考えると、以下のように列挙できます。

$\displaystyle{ y_1 = \sum_i^N w_i \phi_{1, i}\\ \vdots\\ y_N = \sum_i^N w_i \phi_{N, i} }$

ここで簡単のため $\phi_{j, i} = \phi(\mathbf{x}_j, \mathbf{x}_i)$ という表記を用いました。すると、これらは行列形式でまとめて

$\displaystyle{ \mathbf{y} = \Phi \mathbf{w} }$

と書くことができます。ただし $\mathbf{y}$ と $\Phi$ はそれぞれ

$\displaystyle{ \mathbf{y} = \begin{bmatrix} y_1 & \ldots & y_N \end{bmatrix}^T, }$
$\displaystyle{ \Phi = \begin{bmatrix} \phi_{1, 1} & \cdots & \phi_{1, N} \\ \vdots & \ddots & \vdots \\ \phi_{N, 1} & \cdots & \phi_{N, N} \end{bmatrix} }$

を表しているとします。ちなみに $\phi_{j, i} = \phi_{i, j}$ ですから、 $\Phi$ は対称行列になっています。さて、この条件式は $\mathbf{w}$ に関する連立一次方程式と見做すことができ、またほとんどの場合は $\Phi$ には逆行列が存在するので、

$\displaystyle{ \mathbf{w} = \Phi^{-1} \mathbf{y} }$

とすることで解を求めることができます。

C++ による RBF 補間の実装

f:id:yuki-koyama:20180510100442p:plain

C++ による実装例です。行列演算の部分は、外部ライブラリとして Eigen を用いています。

Eigen

重みの計算方法

入力 $(\mathbf{x}_1, y_1), \ldots , (\mathbf{x}_N, y_N)$ に対して重み $\mathbf{w}$ を計算する関数は例えば以下のように書けます。

#include <Eigen/Core>

using namespace Eigen;
using namespace std;

VectorXd compute_weights(const VectorXd& y, const vector<VectorXd>& x)
{
    MatrixXd Phi = MatrixXd::Zero(N, N);
    for (int i = 0; i < N; ++ i) {
        for (int j = 0; j < N; ++ j) {
            Phi(i, j) = phi(x[i], x[j]);
        }
    }
    const VectorXd w = solve_linear_system(Phi, y);
    return w;
}

ここで、RBF を表す関数 phi を以下のように定義しておきます。ここでは $\phi(\mathbf{x})=\left \| \mathbf{x} \right \|$ の定義を用いることにすると、

double phi(const VectorXd& x)
{
    return x.norm();
}

double phi(const VectorXd& x, const VectorXd& c)
{
    return phi(x - c);
}

のようになります。

また一般的な連立一次方程式 $\mathbf{A}\mathbf{x}=\mathbf{b}$ を解くための関数 solve_linear_system は、どのアルゴリズムを用いても良いですが、例えば完全ピボット選択の LU 分解 (LU decomposition with full pivoting) を用いる場合は

#include <Eigen/LU>
VectorXd solve_linear_system(const MatrixXd& A, const VectorXd& b)
{
    FullPivLU<MatrixXd> lu(A);
    const VectorXd x = lu.solve(b);
    return x;
}

のように書きます。今回 $\Phi$ は正定値エルミート行列ですので、コレスキー分解 (Cholesky decomposition) を用いても良いです。一回だけ計算すれば良いとはいえ、この部分の計算量 (時間計算量も空間計算量も) は大きく、例えば $N=10000$ などになると標準的なラップトップで計算するのが困難になることもあるので注意が必要です。

補間結果の値の評価

以上のように求めた重み $\mathbf{w}$ を用いると、任意の入力 $\mathbf{x}_{\mathrm{input}}$ に対する補間結果 $y_{\mathrm{interp}} = f(\mathbf{x}_{\mathrm{input}})$ は以下のように計算できます。

double f(const VectorXd& x_input)
{
    double y_interp = 0.0;
    for (int i = 0; i < N; ++ i) {
        y_interp += w[i] * phi(x_input, x[i]);
    }
    return y_interp;
}

ここからも分かる通り、補間値の評価の処理は RBF Center の数 $N$ に対して計算量は $O(N)$ となっています。一度重みの計算さえしておけば、補間値の評価は $N$ が多少大きくても非常に高速に計算可能です。

ソースコード

以下に C++, Eigen を用いて RBF 補間の機能を実装したライブラリを公開しました。後述する Regularization にも対応しています。

github.com

RBF 補間の応用

Computer Graphics (CG) 分野での応用例

次の 2001 年の SIGGRAPH で発表された論文では

物体表面を表す三次元点群データから滑らかな表面の構築
一部が欠損している表面メッシュデータの穴埋め

の二つの目的を、RBF 補間を応用することで達成しています。

この記事を書いている時点で被引用数が 1300 を超える有名論文で、RBF 補間について詳しく議論しています。

J. C. Carr, R. K. Beatson, J. B. Cherrie, T. J. Mitchell, W. R. Fright, B. C. McCallum, and T. R. Evans.
Reconstruction and Representation of 3D Objects with Radial Basis Functions
SIGGRAPH '01
Reconstruction and representation of 3D objects with radial basis functions

また以下の4本の論文では、次のような処理が行われています。

Measurement-Based Model Fitting. 特定の条件下での実験観測データから、その条件下での物理特性を推定する
Data-Driven Simulation. 推定された特定の条件下における物理特性を RBF Center と見做し、RBF 補間することで、未知の条件下での物理特性を推定し、そのような未知の条件下でも信頼度の高いシミュレーションを行う

後者の過程で scattered data interpolation の考え方が使われており、ここでは RBF 補間が採用されています。

B. Bickel, M. Bächer, M. A. Otaduy, W. Matusik, H. Pfister, and M. Gross.
Capture and Modeling of Non-Linear Heterogeneous Soft Tissue
SIGGRAPH 2009

B. Bickel, M. Bächer, M. A. Otaduy, H. R. Lee, H. Pfister, M. Gross, and W. Matusik.
Design and Fabrication of Materials with Desired Deformation Behavior
SIGGRAPH 2010

N. Umetani, Y. Koyama, R. Schmidt, and T. Igarashi.
Pteromys: Interactive Design and Optimization of Free-formed Free-flight Model Airplanes
SIGGRAPH 2014
http://www.nobuyuki-umetani.com/publication/2014_sigg_pteromys/2014_siggraph_GliderDesign.html

M. Nakamura, Y. Koyama, D. Sakamoto, and T. Igarashi.
An Interactive Design System of Free-Formed Bamboo-Copters
Pacific Graphics 2016
https://mori0501.github.io/projects/BambooCopter/

過学習を避けるための工夫 (Regularization)

先に述べた通り、ナイーブな RBF 補間は過学習のようなことが起き得ます。これを避けるための一つの方法として、weight-decay regularization と呼ばれる手法があります。

f:id:yuki-koyama:20180509093627p:plain

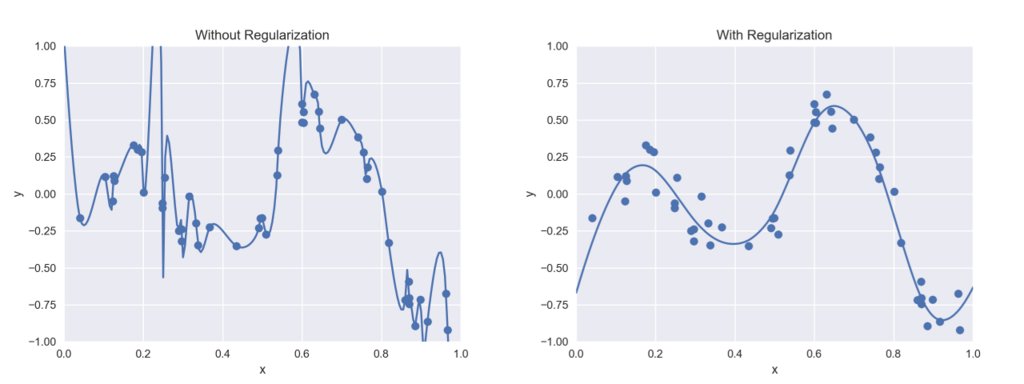
次のページで詳しく説明されています。

rbf-interpolation - mathtoolbox

RBF Center の数を減らすための工夫 (Reduction)

その他の関連用語

Thin Plate Spline (TPS) Interpolation: https://en.wikipedia.org/wiki/Thin_plate_spline
Polyharmonic Spline Interpolation: https://en.wikipedia.org/wiki/Polyharmonic_spline

*1:追記 (2015/07/12): PRML の 6.3 章「RBF ネットワーク」にて次のように紹介されています："歴史的には，RBFが初めて導入されたのは関数補間 (function interpolation) を正確に行うためであった (Powell, 1987)．" (引用元：C.M. ビショップ. 元田他監訳. (2008). パターン認識と機械学習 (下) ベイズ理論による統計的予測. シュプリンガー・ジャパン株式会社.) つまり、RBF 補間という考え方がもともとあり、それをニューラルネットワークとして解釈したときに RBF ネットワークと呼ばれることがあるということだと思います。