Multidimensional Scaling (多次元尺度構成法, MDS) の計算方法と実装

Multidimensional Scaling (MDS) について少し勉強したのでメモしておきます。

Multidimensional Scaling とは

はじめに

日本語では「多次元尺度構成法」と呼ばれる統計テクニックの一つです。英語版ウィキペディアの記事が詳細です。

多次元尺度構成法 - Wikipedia
Multidimensional scaling - Wikipedia

MDS には色々な派生がありますが、ここでは Classical MDS (古典的多次元尺度構成法) と呼ばれる最も基礎的で古典的なものについてのみ記述します。

どういうときに使えるか

いくつか要素があり、要素間の距離がなんらかの形で定義できる場合に、その要素を多次元空間に配置する場合に使えます。

具体例

例えば、いま目の前に日本酒が１０銘柄（鳳凰美田、花陽浴、...）あるとし、これらを一つずつ味見し「どの銘柄とどの銘柄がどのぐらい似ているか（似ていないか）」という指標によって、以下のように任意の２銘柄間の距離が定義できるとします。

要素間の距離の定義のイメージ*1。 $d(\cdot, \cdot)$ は要素間の距離を表すとする。

$d$ (農口, 村祐) $= 2$	$d$ (農口, 鳳凰美田) $= 4$	$d$ (農口, 花陽浴) $= 7$	...
$d$ (十四代, 村祐) $= 2$	$d$ (十四代, 呼友) $= 2$	$d$ (十四代, 花陽浴) $= 5$	...
...	...	...	...

MDS を用いると、これらの距離の情報から、例えば２次元の座標系に銘柄の「マップ」を可視化することができたりします。ここで、各点の座標は MDS によって計算され、その際に各点間の距離は先ほど定義した距離が反映されます。

f:id:yuki-koyama:20150712143405p:image:w420

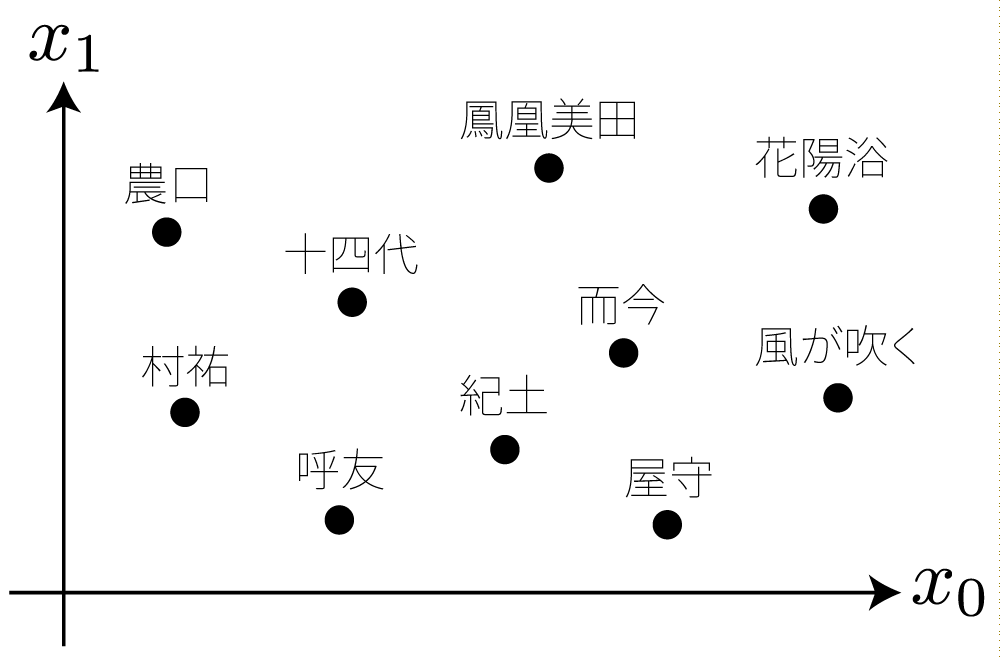
MDS の使用イメージ*2。MDS によって各点の座標が計算される。

入力と出力

MDS の入力は要素間の距離と、対象とする空間の次元です。一般的には、距離は距離行列 (distance matrix) として表現しておきます。要素数が $n$ であった場合、 $D_{i,j}$ が $i$ 番目と $j$ 番目の要素の距離の二乗*3であるような正方行列 $\mathbf{D} \in \mathbb{R}^{n \times n}$ が入力です。このとき、距離の対称性と非退化性*4から、 $\mathbf{D}$ は対角成分が $0$ であるような対称行列となります。

MDS の出力は、各要素の座標 $(\mathbf{x}_1, \ldots, \mathbf{x}_n)$ です。ここで、指定された空間の次元が $m$ だとすると、 $\mathbf{x}_i \in \mathbb{R}^m$ です。これらは $i$ 番目の行を $\mathbf{x}_i$ とする行列 $\mathbf{X} \in \mathbb{R}^{m \times n}$ として表現したりします*5。

次元圧縮 (Low-Dimensional Embedding)

高次元の点群データから距離行列 $\mathbf{D}$ を計算し、元の次元よりも小さな次元 $m$ を指定し MDS を実行することで、次元圧縮 (Low-Dimensional Embedding) を実現することができたりもします*6。

非線形な次元圧縮手法としてよく使われる ISOMAP も MDS を拡張したものです。

MDS の計算方法

行列 $\mathbf{X}$ を求めるためには、まず

$\mathbf{K} = \mathbf{X}^T\mathbf{X} \in \mathbb{R}^{n \times n}$
を満たす行列 $\mathbf{K}$ *7 *8を、入力として与えられた距離行列 $\mathbf{D}$ から計算できるとします。すると、この行列 $\mathbf{K}$ は固有値分解 (eigenvalue decomposition) によって
$\mathbf{K} = \mathbf{V}\mathbf{\Lambda}\mathbf{V}^T$
と分解することができます*9 *10。ここで $\mathbf{V}$ は固有ベクトルを並べた行列、 $\mathbf{\Lambda}$ は固有値を対角成分に持つ行列です。これらを用いて、
$\mathbf{X} = \mathrm{sqrt}(\mathbf{\Lambda})\mathbf{V}^T$
とすることで、所望の $\mathbf{X}$ を計算することができます*11。ここで $\mathrm{sqrt}(\cdot)$ は要素毎に累乗根をとることを意味しています*12。また、このままでは空間の次元は $n$ ですが、これをより小さい次元 $m$ に削減するには、固有値の上位 $m$ 個と、それに対応する固有ベクトルのみを使って前式を計算することで実現できます*13。

与えられた距離行列 $\mathbf{D}$ からカーネル行列 $\mathbf{K}$ を計算する方法ですが、これは

$\mathbf{K} = - \frac{1}{2} \mathbf{H} \mathbf{D} \mathbf{H}$
によって算出するようです。ただし
$\mathbf{H} = \mathbf{I} - \frac{1}{n}\mathbf{1}\mathbf{1}^T$
は中心化行列*14と呼ばれ、得られる結果の原点を重心に移す効果があるそうです*15 *16。

MDS の実装

C++ によって MDS を実装した例を以下に示します。行列演算ライブラリとして Eigen を用いています。

#include <Eigen/Core>
#include <vector>
#include <utility>
using namespace std;
using namespace Eigen;

// This function computes low-dimensional embedding by using multi-dimensional scaling (MDS)
// - Input:  A distance (dissimilarity) matrix and a target dimension for embedding
// - Output: A coordinate matrix whose i-th column corresponds to the embedded coordinates of the i-th entry
MatrixXd computeMDS(const MatrixXd &D, unsigned dim)
{
    assert(D.rows() == D.cols());
    assert(D.rows() >= dim);
    const unsigned n = D.rows();
    const MatrixXd H = MatrixXd::Identity(n, n) - (1.0 / static_cast<double>(n)) * VectorXd::Ones(n) * VectorXd::Ones(n).transpose();
    const MatrixXd K = - 0.5 * H * D * H;
    const EigenSolver<MatrixXd> solver(K);
    VectorXd S = solver.eigenvalues().real();
    MatrixXd V = solver.eigenvectors().real();
    extractNLargestEigen(dim, S, V);
    const MatrixXd X = DiagonalMatrix<double, Dynamic>(sqrt(S)) * V.transpose();
    return X;
}

以下にテストコード等を含めた git repository 公開しました：
github.com

参考にした文献

ウェブ検索等で見つけた以下の文献を、それぞれ断片的に参考にしつつ勉強しました（特に参考にした順にソート）：

他によくまとまっている文献などがあれば是非ご教示ください。

*1:これらの銘柄は実在するものですが、その距離として与えられている値には全く根拠はなく、極めて乱数に近いものであると考えてください。

*2:この図はあくまでイメージを掴むためのもので、実際のデータから計算されたものではありません。

*3:この部分について明示していない文献も多く私は途中まで勘違いしていたのですが、距離行列は距離の二乗を要素として持つようです。

*4:距離空間 - Wikipedia

*5:文献によっては $i$ 番目の列を $\mathbf{x}_{i}^T$ とする行列 $\mathbf{X} \in \mathbb{R}^{n \times m}$ として表現したりすることもあります。

*6:この操作は Principal Component Analysis (PCA) と同値？

*7:グラム行列（PRML 6.2章）

*8:文献によって $\mathbf{B}$ と表記されることもあります。

*9: $\mathbf{K}$ は対称行列であるため、特異値分解 (SVD) を用いても同様の計算ができます。

*10: $\mathbf{D}$ がユークリッド距離に基づいているとき、まとそのようなときに限り $\mathbf{K}$ は半正定値行列となる？

*11: $\mathbf{X}^T\mathbf{X} = (\mathrm{sqrt}(\mathbf{\Lambda})\mathbf{V}^T)^T (\mathrm{sqrt}(\mathbf{\Lambda})\mathbf{V}^T) = \mathbf{V} \mathrm{sqrt}(\mathbf{\Lambda}) \mathrm{sqrt}(\mathbf{\Lambda}) \mathbf{V}^T = \mathbf{V}\mathbf{\Lambda}\mathbf{V}^T$