ゲームなどで使われるリアルタイムの流体シミュレーションといえば SPH (Smoothed Particle Hydro-dynamics) に基づく手法が有名です。SPH という考え方自体は古くからあるのですが、2003 年に Muller らが SCA という会議で発表した論文をきっかけに、コンピュータグラフィクス分野で広く使われるようになりました。

SPH は簡単にいうと粒子間の影響を補間する手法です。

背景２：Position-Based Dynamics (PBD)

流体シミュレーションとは別の文脈で、同じく Muller らが 2006 年に提案した物理シミュレーションのための枠組みで PBD (Position-Based Dynamics) と呼ばれる手法があります。これは従来の陽的オイラー法よりも安定でかつ陰的オイラー法よりも高速な時間積分 (Verlet) を利用しており、NVIDIA PhysX, Maya, Houdini でも採用されています。

yuki-koyama.hatenablog.com

PBD は、物体の振る舞いを力を用いて表現するのではなく、位置に基づく制約として表現する枠組みになっています。

Position-Based Fluids

今回の対象となる Position-Based Fluids もまた同じく Muller らによって 2013 年に提案されました。Position-Based Fluids を多少乱暴にいうと「PBD の枠組みの中で動く SPH 法」という感じです（流体の専門家には怒られるかもしれません）。SPH 法ではナビエストークス方程式から粒子に働く力を表現していたのに対し、Position-Based Fluids では流体の非圧縮性を位置に基づく制約として表現することで粒子の振る舞いを決定します。

具体的には以下の制約を考えます。

$\displaystyle{ C_i (\mathbf{p}_1, \ldots, \mathbf{p}_n) = \frac{\rho_i}{\rho_0} - 1 }$
ここで $i$ は粒子のインデックス、 $\mathbf{p}_i$ は $i$ 番目の粒子の位置、 $\rho_i$ は $i$ 番目の粒子周りの密度、 $\rho_0$ はこの流体の通常の状態での密度です。できるだけ $C_i=0 \:\:(i=1, \ldots, n)$ となるように粒子の位置を決定することで、流体の振る舞いを表現します。ここで、 $\rho_i$ を推定する部分で SPH のアイデアを用いています。

実装した感想

Unity はプロトタイピングにすごく便利。可視化の部分のコードを書かなくても Unity がやってくれる。
近傍探索の高速化は必須。ナイーブな実装だと $O(n^2)$ で効いてくるのですぐに計算が重くなってしまう。
GPU 化は必須。弾性体シミュレーションや剛体シミュレーションに比べ流体シミュレーションは自由度が大きくなりがちなため、すぐに計算が重くなってしまう。PBD や Position-Based Fluids は GPU-Friendly なので GPU 実装するべき。
水面の復元を実装するのはすこし大変そう。特に論文では GPU 実装しているが、これは結構大変そう。
本気で全てを実装すると数ヶ月はかかりそう。

対話型機械学習 (Interactive Machine Learning, IML) について

機械学習 HCI

普段は Computer Graphics や Human-Computer Interaction を勉強しているのですが、最近は機械学習も少し勉強しています。今回は Human-Computer Interaction とも関わりの深いトピックである「対話型機械学習 (Interactive Machine Learning, IML)」について簡単にまとめます。

参考文献

ある機械学習の専門家にこちらの記事をおすすめされました。

Saleema Amershi, Maya Cakmak, W. Bradley Knox, Todd Kulesza:
Power to the People: The Role of Humans in Interactive Machine Learning.
AI Magazine 35(4): 105-120 (2014)
PDF download

この文献は interactive machine learning のサーベイというよりは、この分野を知らない人のための教科書的な導入として書かれているようです。

Interactive Machine Learning とは

そもそも伝統的な機械学習は

[...] a powerful tool for transforming data into computational models that can drive user-facing applications.

です。つまり、データがあって、ユーザがいるわけですが、ここで問題となるのはこの "computational models" を構築する作業は肝心のユーザではなく別の "skilled practitioners" (データサイエンティスト？) が行うという点です。したがって、この "practitioners" は実際のユーザと打ち合わせをしながら、適切な特徴量選択やパラメタチューニングを反復的に行っていく必要がありました。

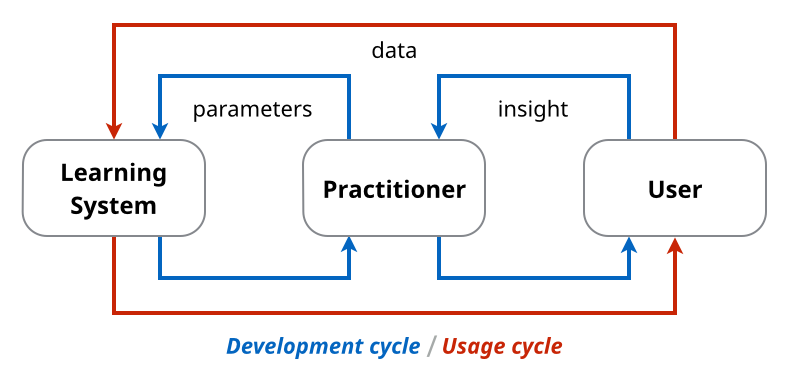
伝統的な機械学習ではユーザが直接モデル構築を行わないため学習と使用が乖離している。

伝統的な機械学習に対し、モデル構築の過程で直接ユーザと対話することで、より良いユーザエクスペリエンスやより効果的な学習機構を目指すものを interactive machine learning と呼ぶようです。これによって、例えば "practitioners" を挟む間接的なやり方よりも、直接学習と使用のサイクルを回すことができます。

Interactive Machine Learning ではユーザが直接モデル構築に関与する。

文献の中では、伝統的な機械学習と比較した際の interactive machine learning の特徴として、以下の三点が挙げられています。

モデルの更新がより rapid である（ユーザ入力に対し即座にモデルを更新する）
モデルの更新がより focused である（モデルの特定の側面だけが更新される）
モデルの更新がより incremental である（一回の更新の大きさが小さく、劇的に変わることがない）

これらの条件が満たされることによって、機械学習の専門家でないユーザでも "low-cost trial-and-error or focused experimentation with inputs and outputs" をすることができ、効果的になると述べられています。

事例：画像のセグメンテーションにおける Interactive Machine Learning

Human-computer interaction の文脈において interactive machine learning という言葉が初めて使われたのは以下の論文だそうです：

Jerry Alan Fails and Dan R. Olsen, Jr..
Interactive machine learning.
In Proc. IUI '03. (Best Paper Award)
PDF download

この研究は画像のセグメンテーション（ここでは前景と背景を分ける）において、ユーザが前景（または背景）のピクセル群をブラシストロークによって対話的にマークしていくことで classifier の学習を進めていくという手法が提案されています。

これはちょうど Adobe Photoshop CC 2015 などに搭載されている「クイック選択ツール」の挙動と似ていると思います：

また、この研究で行われたユーザスタディにおいて得られた重要な知見の一つとして、システムの挙動（その時点での classifier によって得られるセグメンテーションの可視化）に応じてユーザが挙動（どこを次にマークするか）を変えた、という点が挙げられます。具体的には、システムがセグメンテーションに失敗した部分をユーザが直す、ということが行われたそうです。この事実は、interactive machine learning では interaction design が学習の効果に大きく寄与するということを示唆していると考えられます。

Interactive Machine Learning に関する学会・会議など

Interactive machine learning の研究は主に CHI, UIST, IUI などの human-computer interaction に関する国際会議で発表されることが多いようです。これは、学習で用いられるモデルそのものよりも、interaction design における知見や human factor の扱いに関する知見が interactive machine learning においては大きな課題であるからだと思われます。

2015-07-19

共分散行列を含む多次元のガウス関数の微分

数学機械学習

目的：ガウス関数の微分

共分散行列 $\mathbf{\Sigma}$ (バンド幅行列) を用いて表された多次元 (多変量) で異方性のガウス関数 (多変量正規分布) の微分 (勾配) を考えます。微分したいガウス関数の形は

$\displaystyle{ \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) = \frac{1}{(2\pi)^{\frac{n}{2}}|\mathbf{\Sigma}|^{\frac{1}{2}}}\exp\left( - \frac{1}{2} (\mathbf{x - {\boldsymbol \mu}})^T \mathbf{\Sigma}^{-1} (\mathbf{x - {\boldsymbol \mu}})\right) }$
だとします。ただし $\mathbf{\Sigma} \in \mathbb{R}^{n \times n}$ は正値対称な共分散行列 (バンド幅行列) で、 $\mathbf{x}, {\boldsymbol \mu} \in \mathbb{R}^n$ です。これはPRMLなどの機械学習の参考書でも見られるガウス分布の表し方です。

f:id:yuki-koyama:20150719182454p:image:w360

共分散行列を $\mathbf{\Sigma}$ 、中心を ${\boldsymbol \mu}$ とするような多次元のガウス関数 $\mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma})$ のイメージ。

ちなみにバンド幅が $\sigma \in \mathbb{R}$ によって表された $\mu \in \mathbb{R}$ を中心とする 1 次元のガウス関数

$\displaystyle{ \mathcal{N}(x; \mu, \sigma) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left(- \frac{(x - \mu)^2}{2\sigma^2} \right) }$
の微分は

などでも紹介されている通り、

$\displaystyle{ \frac{d}{dx}\mathcal{N}(x; \mu, \sigma) = - \frac{x - \mu}{\sqrt{2\pi}\sigma^3} \exp\left(- \frac{(x - \mu)^2}{2\sigma^2} \right) }$
となります。今回はこれの $n$ 次元への拡張、さらにバンド幅が等方性ではなく異方性のものを微分します。

準備：指数部にベクトル・行列が含まれるときのベクトルによる微分

$\mathbf{x}$ を $n \times 1$ ベクトル、 $\mathbf{A}$ を $n \times n$ 対称行列とするとき、

$\displaystyle{ \frac{\partial}{\partial \mathbf{x}} \left( \mathbf{x}^T \mathbf{A} \mathbf{x} \right) = 2 \mathbf{A} \mathbf{x} }$
が成り立ちます。この公式自体は様々な記事やウェブサイトで紹介されているので、ウェブ検索をかけるとすぐに見つかります。

この公式と合成関数の微分の公式 (Chain Rule) を用いることで、

$\displaystyle{ \frac{\partial}{\partial \mathbf{x}} \left\{ \exp \left( - \frac{1}{2}\mathbf{x}^T \mathbf{A}\mathbf{x} \right) \right\} \\ = \frac{\partial y}{\partial \mathbf{x}} \cdot \frac{\partial}{\partial y} \exp(y) \:\:\: \left( y := - \frac{1}{2}\mathbf{x}^T\mathbf{A}\mathbf{x} \right) \\ = - \frac{1}{2} \cdot \frac{\partial}{\partial \mathbf{x}} \left( \mathbf{x}^T\mathbf{A}\mathbf{x} \right) \cdot \exp(y) \\ = - \frac{1}{2} \cdot 2 \mathbf{A} \mathbf{x} \cdot \exp \left( - \frac{1}{2}\mathbf{x}^T\mathbf{A}\mathbf{x} \right) \\ = - \exp \left( - \frac{1}{2} \mathbf{x}^T \mathbf{A} \mathbf{x} \right) \mathbf{A} \mathbf{x} }$
という関係式を導くことができます。この式は

http://sci-tech.ksc.kwansei.ac.jp/~inagai/write/write_index.html

では公式として紹介されています。ちなみにベクトルによる微分の Chain Rule は

http://www.colorado.edu/engineering/CAS/courses.d/IFEM.d/IFEM.AppF.d/IFEM.AppF.pdf

で証明が紹介されています。

導出：式変形と結果

上記で導いた関係式と再び合成関数の微分の公式 (Chain Rule) を用いると

$\displaystyle{ \frac{\partial}{\partial \mathbf{x}} \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \\ = \frac{1}{(2\pi)^{\frac{n}{2}}|\mathbf{\Sigma}|^{\frac{1}{2}}} \cdot \frac{\partial}{\partial \mathbf{x}} \exp\left( - \frac{1}{2} (\mathbf{x - {\boldsymbol \mu}})^T \mathbf{\Sigma}^{-1} (\mathbf{x - {\boldsymbol \mu}})\right) \\ = \frac{1}{(2\pi)^{\frac{n}{2}}|\mathbf{\Sigma}|^{\frac{1}{2}}} \cdot \frac{\partial \mathbf{z}}{\partial \mathbf{x}} \cdot \frac{\partial}{\partial \mathbf{z}} \exp\left( - \frac{1}{2} \mathbf{z}^T \mathbf{\Sigma}^{-1} \mathbf{z} \right) \:\:\: \left( \mathbf{z} := \mathbf{x} - {\boldsymbol \mu} \right) \\ = \frac{1}{(2\pi)^{\frac{n}{2}}|\mathbf{\Sigma}|^{\frac{1}{2}}} \cdot \mathbf{I} \cdot \left\{ - \exp\left( - \frac{1}{2} \mathbf{z}^T \mathbf{\Sigma}^{-1} \mathbf{z} \right) \mathbf{\Sigma}^{-1} \mathbf{z} \right\} \\ = - \frac{1}{(2\pi)^{\frac{n}{2}}|\mathbf{\Sigma}|^{\frac{1}{2}}} \exp\left( - \frac{1}{2} (\mathbf{x} - {\boldsymbol \mu})^T \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right) \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \\ = - \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) }$
が得られます。また、冒頭で紹介した 1 次元のガウス関数の微分の関係式
$\displaystyle{ \frac{d}{dx}\mathcal{N}(x; \mu, \sigma) = - \frac{x - \mu}{\sqrt{2\pi}\sigma^3} \exp\left(- \frac{(x - \mu)^2}{2\sigma^2} \right) }$
も、得られた式において $\mathbf{\Sigma}$ を $\sigma^2$ で置き換え $n=1$ とすることで、確かに成り立っていることが分かります。

おまけ：二階微分（ヘッセ行列）

上記で得られた結果をさらに用いて、ガウス関数のヘッセ行列 (Hessian Matrix) を求めます。

ベクトル $\mathbf{x}$ を引数とするスカラー関数 $f(\mathbf{x})$ のヘッセ行列 $\mathbf{H}$ は

で説明されている通り、

$\displaystyle{ \mathbf{H} = \frac{\partial^2}{\partial \mathbf{x} \partial \mathbf{x}^T} f(\mathbf{x}) = \frac{\partial}{\partial \mathbf{x}} \left( \frac{\partial}{\partial \mathbf{x}} f(\mathbf{x}) \right)^T }$
で計算されます。したがって、ガウス関数のヘッセ行列は
$\displaystyle{ \mathbf{H} = \frac{\partial^2}{\partial \mathbf{x} \partial \mathbf{x}^T} \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \\ = \frac{\partial}{\partial \mathbf{x}} \left\{ \frac{\partial}{\partial \mathbf{x}} \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \right\}^T \\ = \frac{\partial}{\partial \mathbf{x}} \left\{ - \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right\}^T \\ = - \left\{ \frac{\partial}{\partial \mathbf{x}} \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \right\} \left( \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right)^T - \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \left\{ \frac{\partial}{\partial \mathbf{x}} \left( \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right)^T \right\} \\ = - \left( - \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right) \left( \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) \right)^T - \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \mathbf{\Sigma}^{-1} \\ = \mathcal{N}(\mathbf{x}; {\boldsymbol \mu}, \mathbf{\Sigma}) \left\{ \mathbf{\Sigma}^{-1} (\mathbf{x} - {\boldsymbol \mu}) (\mathbf{x} - {\boldsymbol \mu})^T \mathbf{\Sigma}^{-1} - \mathbf{\Sigma}^{-1} \right\} }$
となります。途中、 $(\mathbf{\Sigma}^{-1})^T = \mathbf{\Sigma}^{-1}$ が成り立つことと、ベクトルによる微分に関する積の微分の関係式を用いました。一階微分を計算したときと同様に、 $\mathbf{\Sigma}$ を $\sigma^2$ で置き換え $n=1$ とすることで

http://www.ms.is.ritsumei.ac.jp/profile/staff/ijiri/study/gaussianDerivatives.html

で示されている結果などと矛盾しないことが分かります。

最後に

この記事には間違いがある可能性があります。ここに書かれている数式を用いる場合には必ず自身で再計算して確認してからにしてください。また、もし間違いを見つけた場合には教えてください。

2015-07-13

Multidimensional Scaling (多次元尺度構成法, MDS) の計算方法と実装

数学ソースコード開発機械学習

Multidimensional Scaling (MDS) について少し勉強したのでメモしておきます。

Multidimensional Scaling とは

はじめに

日本語では「多次元尺度構成法」と呼ばれる統計テクニックの一つです。英語版ウィキペディアの記事が詳細です。

多次元尺度構成法 - Wikipedia
Multidimensional scaling - Wikipedia

MDS には色々な派生がありますが、ここでは Classical MDS (古典的多次元尺度構成法) と呼ばれる最も基礎的で古典的なものについてのみ記述します。

どういうときに使えるか

いくつか要素があり、要素間の距離がなんらかの形で定義できる場合に、その要素を多次元空間に配置する場合に使えます。

具体例

例えば、いま目の前に日本酒が１０銘柄（鳳凰美田、花陽浴、...）あるとし、これらを一つずつ味見し「どの銘柄とどの銘柄がどのぐらい似ているか（似ていないか）」という指標によって、以下のように任意の２銘柄間の距離が定義できるとします。

要素間の距離の定義のイメージ*1。 $d(\cdot, \cdot)$ は要素間の距離を表すとする。

$d$ (農口, 村祐) $= 2$	$d$ (農口, 鳳凰美田) $= 4$	$d$ (農口, 花陽浴) $= 7$	...
$d$ (十四代, 村祐) $= 2$	$d$ (十四代, 呼友) $= 2$	$d$ (十四代, 花陽浴) $= 5$	...
...	...	...	...

MDS を用いると、これらの距離の情報から、例えば２次元の座標系に銘柄の「マップ」を可視化することができたりします。ここで、各点の座標は MDS によって計算され、その際に各点間の距離は先ほど定義した距離が反映されます。

f:id:yuki-koyama:20150712143405p:image:w420

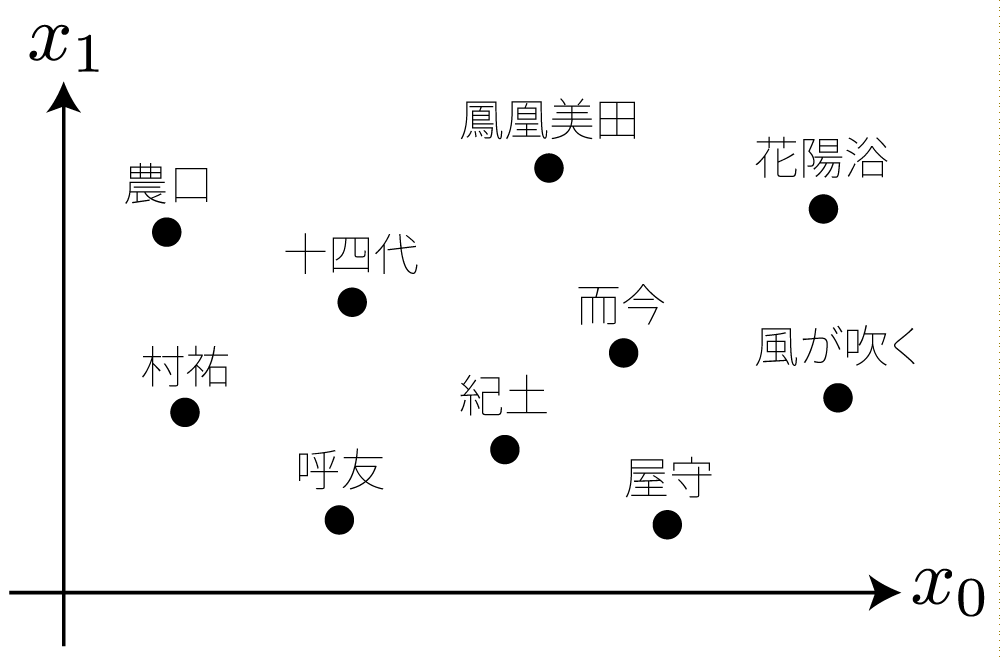
MDS の使用イメージ*2。MDS によって各点の座標が計算される。

入力と出力

MDS の入力は要素間の距離と、対象とする空間の次元です。一般的には、距離は距離行列 (distance matrix) として表現しておきます。要素数が $n$ であった場合、 $D_{i,j}$ が $i$ 番目と $j$ 番目の要素の距離の二乗*3であるような正方行列 $\mathbf{D} \in \mathbb{R}^{n \times n}$ が入力です。このとき、距離の対称性と非退化性*4から、 $\mathbf{D}$ は対角成分が $0$ であるような対称行列となります。

MDS の出力は、各要素の座標 $(\mathbf{x}_1, \ldots, \mathbf{x}_n)$ です。ここで、指定された空間の次元が $m$ だとすると、 $\mathbf{x}_i \in \mathbb{R}^m$ です。これらは $i$ 番目の行を $\mathbf{x}_i$ とする行列 $\mathbf{X} \in \mathbb{R}^{m \times n}$ として表現したりします*5。

次元圧縮 (Low-Dimensional Embedding)

高次元の点群データから距離行列 $\mathbf{D}$ を計算し、元の次元よりも小さな次元 $m$ を指定し MDS を実行することで、次元圧縮 (Low-Dimensional Embedding) を実現することができたりもします*6。

非線形な次元圧縮手法としてよく使われる ISOMAP も MDS を拡張したものです。

MDS の計算方法

行列 $\mathbf{X}$ を求めるためには、まず

$\mathbf{K} = \mathbf{X}^T\mathbf{X} \in \mathbb{R}^{n \times n}$
を満たす行列 $\mathbf{K}$ *7 *8を、入力として与えられた距離行列 $\mathbf{D}$ から計算できるとします。すると、この行列 $\mathbf{K}$ は固有値分解 (eigenvalue decomposition) によって
$\mathbf{K} = \mathbf{V}\mathbf{\Lambda}\mathbf{V}^T$
と分解することができます*9 *10。ここで $\mathbf{V}$ は固有ベクトルを並べた行列、 $\mathbf{\Lambda}$ は固有値を対角成分に持つ行列です。これらを用いて、
$\mathbf{X} = \mathrm{sqrt}(\mathbf{\Lambda})\mathbf{V}^T$
とすることで、所望の $\mathbf{X}$ を計算することができます*11。ここで $\mathrm{sqrt}(\cdot)$ は要素毎に累乗根をとることを意味しています*12。また、このままでは空間の次元は $n$ ですが、これをより小さい次元 $m$ に削減するには、固有値の上位 $m$ 個と、それに対応する固有ベクトルのみを使って前式を計算することで実現できます*13。

与えられた距離行列 $\mathbf{D}$ からカーネル行列 $\mathbf{K}$ を計算する方法ですが、これは

$\mathbf{K} = - \frac{1}{2} \mathbf{H} \mathbf{D} \mathbf{H}$
によって算出するようです。ただし
$\mathbf{H} = \mathbf{I} - \frac{1}{n}\mathbf{1}\mathbf{1}^T$
は中心化行列*14と呼ばれ、得られる結果の原点を重心に移す効果があるそうです*15 *16。

MDS の実装

C++ によって MDS を実装した例を以下に示します。行列演算ライブラリとして Eigen を用いています。

#include <Eigen/Core>
#include <vector>
#include <utility>
using namespace std;
using namespace Eigen;

// This function computes low-dimensional embedding by using multi-dimensional scaling (MDS)
// - Input:  A distance (dissimilarity) matrix and a target dimension for embedding
// - Output: A coordinate matrix whose i-th column corresponds to the embedded coordinates of the i-th entry
MatrixXd computeMDS(const MatrixXd &D, unsigned dim)
{
    assert(D.rows() == D.cols());
    assert(D.rows() >= dim);
    const unsigned n = D.rows();
    const MatrixXd H = MatrixXd::Identity(n, n) - (1.0 / static_cast<double>(n)) * VectorXd::Ones(n) * VectorXd::Ones(n).transpose();
    const MatrixXd K = - 0.5 * H * D * H;
    const EigenSolver<MatrixXd> solver(K);
    VectorXd S = solver.eigenvalues().real();
    MatrixXd V = solver.eigenvectors().real();
    extractNLargestEigen(dim, S, V);
    const MatrixXd X = DiagonalMatrix<double, Dynamic>(sqrt(S)) * V.transpose();
    return X;
}

以下にテストコード等を含めた git repository 公開しました：
github.com

参考にした文献

ウェブ検索等で見つけた以下の文献を、それぞれ断片的に参考にしつつ勉強しました（特に参考にした順にソート）：

他によくまとまっている文献などがあれば是非ご教示ください。

*1:これらの銘柄は実在するものですが、その距離として与えられている値には全く根拠はなく、極めて乱数に近いものであると考えてください。

*2:この図はあくまでイメージを掴むためのもので、実際のデータから計算されたものではありません。

*3:この部分について明示していない文献も多く私は途中まで勘違いしていたのですが、距離行列は距離の二乗を要素として持つようです。

*4:距離空間 - Wikipedia

*5:文献によっては $i$ 番目の列を $\mathbf{x}_{i}^T$ とする行列 $\mathbf{X} \in \mathbb{R}^{n \times m}$ として表現したりすることもあります。

*6:この操作は Principal Component Analysis (PCA) と同値？

*7:グラム行列（PRML 6.2章）

*8:文献によって $\mathbf{B}$ と表記されることもあります。

*9: $\mathbf{K}$ は対称行列であるため、特異値分解 (SVD) を用いても同様の計算ができます。

*10: $\mathbf{D}$ がユークリッド距離に基づいているとき、まとそのようなときに限り $\mathbf{K}$ は半正定値行列となる？

*11: $\mathbf{X}^T\mathbf{X} = (\mathrm{sqrt}(\mathbf{\Lambda})\mathbf{V}^T)^T (\mathrm{sqrt}(\mathbf{\Lambda})\mathbf{V}^T) = \mathbf{V} \mathrm{sqrt}(\mathbf{\Lambda}) \mathrm{sqrt}(\mathbf{\Lambda}) \mathbf{V}^T = \mathbf{V}\mathbf{\Lambda}\mathbf{V}^T$

*12:ただし、 $\mathbf{K}$ が半正定値行列でない場合には固有値に負の値が現れます。その場合はその固有値を 0 だとみなして以降の計算を行います。これはある種の近似を行っていると考えられるそうです。

*13:そのようにして良い根拠はこの資料で説明されています。

*14:文献によって $\mathbf{G}$ と表記されることもあります。

*15:このあたりはよく理解できていませんが、距離を一定に保った点群には剛体移動（平行移動と回転移動）の自由度があるので、そのうち平行移動については重心が原点にくるように制約をかけるということだと思います。

*16:この変換は「ダブル・センタリング変換」と呼ばれる？

yuki-koyama's blog

論文読み: Position Based Fluids (SIGGRAPH '13) その２

実装してみた

論文の概要

背景１：Smoothed Particle Hydro-Dynamics (SPH) 法