追実装: Projective Dynamics (SIGGRAPH 2014)

この記事の概要

現在用いられる物理エンジンの多くは position-based dynamics (PBD) [Muller et al. 2007] を基礎としている *1
近年提案された projective dynamics [Bouaziz et al. 2014] は PBD より優れた性質を持っているらしい
そこで projective dynamics の追実装を行った上で、その将来性について検討する

Projective dynamics による布のシミュレーション

なお projective dynamics は以下の記事でも取り上げたことがあります。今回は前回よりさらにマニアックな内容になっています。

論文読み: Projective Dynamics: Fusing Constraint Projections for Fast Simulation (SIGGRAPH 2014) - yuki-koyama's blog

PBD については以下の記事で取り上げています。

アルゴリズム解説

準備：Implicit Euler Integration (Section 3.1)

Projective dynamics は implicit Euler integration (後退オイラー積分法) に基づく手法です。したがって数値的に安定な性質があります。

まず運動方程式に implicit Euler integration を適用すると、時刻 $t_{n}$ における状態 *2 と時刻 $t_{n+1}$ における状態の関係式を得ることができます。

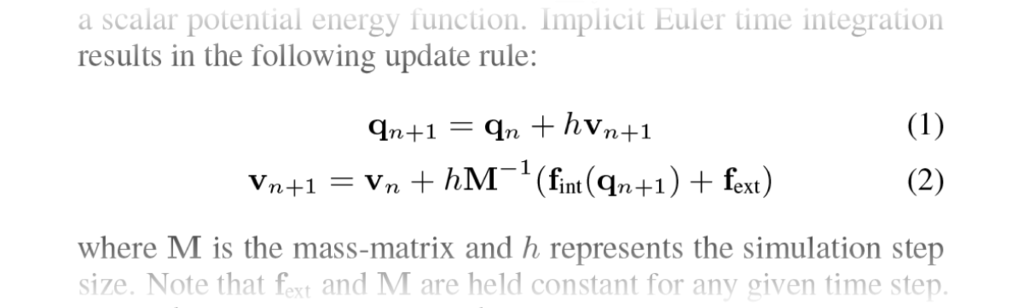
時刻 $t_{n}$ における状態を既知として時刻 $t_{n+1}$ における状態を未知とすると、この関係式は連立方程式とみなすことができます。これを解くのが目標です。

ここで Martin et al. [2011] が提案した式変形を用いることで、この方程式はエネルギー最小化問題 (最適化問題) として定式化することができます。

この目的関数は、

慣性エネルギーに関する項
弾性エネルギー *3 に関する項

の和となっています。慣性に関する項は単純な quadratic ですが、弾性エネルギーに関する項は通常非線形であり *4、このエネルギー最小化問題を高速に解くのは難しいです。

Non-Linear Elasticity (Section 3.2)

そこでこの論文では、非線形な弾性エネルギーの扱いについて新しい考え方を導入します。

通常の連続体力学における超弾性体 *5 の扱いにおいては、弾性変形状態 $\mathbf{q}$ は歪み (strain) $\mathbf{E}(\mathbf{q})$ *6 として表現され、これと材料の歪みエネルギー密度関数 (strain energy density function) *7 を用いることで、弾性エネルギー $W(\mathbf{q})$ が計算されます。

この論文では弾性エネルギー $W(\cdot)$ を、

歪みに関する制約を充たす変形状態がなす多様体 (constraint manifold): $\mathbf{E(\cdot) = \mathbf{0}}$
二つの変形状態間の距離関数: $d(\cdot, \cdot)$

という、二つの要素で定義し直します。より具体的には、

$\displaystyle{ W(\mathbf{q}) = \min_{\mathbf{p}} \left\{ d(\mathbf{q}, \mathbf{p}) + \delta_{\mathbf{E}} (\mathbf{p}) \right\} }$

と弾性エネルギーを定義し直しています。ここで

$\displaystyle{ \delta_{\mathbf{E}}(\mathbf{p}) = \left\{ \begin{array}{ll} 0 & (\mathbf{E}(\mathbf{p}) = 0) \\ + \infty & (\text{otherwise}) \end{array} \right. }$

であり、 $\mathbf{p}$ は多様体のうちで $\mathbf{q}$ に最も近い変形状態を探すための補助変数です。このように表現すると、弾性エネルギーの計算は

現在の変形状態を constraint manifold に投影 (projection) する *8
現在の変形状態と投影後の変形状態の距離を計算する

の二つの処理を行うことで実現できるということになります。

この処理を高速に行うために、projective dynamics では距離関数 $d(\cdot, \cdot)$ を $\mathbf{p}, \mathbf{q}$ に対して quadratic に定義することにします。つまり

$\displaystyle{ d(\mathbf{p}, \mathbf{q}) = \| \mathbf{A} \mathbf{p} - \mathbf{B}\mathbf{q} \|_{F}^2 }$

の形式 *9 で表せるとします。

なお quadratic な距離関数に制限してしまうことのデメリットについては、

The constraint nonlinearity (also known as geometric nonlinearity) is already taken care of by the projection on the constraint set, so the distance metric can be kept simple, trading general material nonlinearity against efficiency and robustness.

と説明されています。つまり、材料の非線形性 (material nonlinearity) は表現できなくなってしまうものの、制約の非線形性 (constraint nonlinearity) は考慮されているから良いだろうということのようです。

Projective Implicit Euler Solver (Section 3.3)

上述の弾性エネルギーの定義を用いると、エネルギー最小化問題として表現された運動方程式は

Local solve: 投影 (projection) によって $\mathbf{p}$ を探す
Global solve: $\mathbf{p}$ を固定した上で $\mathbf{q}_{n+1}$ に関して最小化問題を解く

の二つの処理を繰り返すことで解くことができるようになります。繰り返しの回数を増やすほど真の解に収束していきます。この考え方は global/local alternating optimization または block coordinate descent と呼ばれます *10。

Local solve は制約に対して並列化が可能です。具体的に何を計算するかは後で (論文では Section 5) 説明されます。

Global solve は目的関数が $\mathbf{q}_{n+1}$ に対して quadratic であるため、目的関数を $\mathbf{q}_{n+1}$ で微分した値が $\mathbf{0}$ になるという性質を用いると、線形方程式として解くことができます。さらにこの線形方程式は、係数行列 *11 が時間不変である *12 ため、最初に一度だけ行列の分解を行っておけば、各タイムステップでは高速に計算することが可能となります。

連続体ベースの制約条件 (Section 5)

この論文では projective dynamics で扱える連続体ベースの制約として

Edge strain 制約 (Liu et al. [2013] の手法に類似)
Triangle strain 制約 (Chao et al. [2010] や Wang et al. [2010] の手法に類似)
Tetrahedron strain 制約
面積保存制約
体積保存制約
例示ベース弾性制約 (Martin et al. [2011] や Koyama et al. [2012] の手法に類似)
Bending 制約

などをまとめて提案しています。

これらの連続体ベースの制約は、既存の多くの幾何ベースの制約 *13 と異なり、メッシュの解像度の変化や非一様性に対してロバストに動作するという特徴があります。

その他の制約条件 (Section 6)

この論文では、連続体ベースの制約以外の制約として

位置制約 (ある頂点を引っ張る、空間に固定する、などの用途に使用)
衝突制約

などを説明しています。

さらに、projective dynamics は PBD の一般化であるため、おそらく PBD で用いられる制約 *14 は全て組み込むことが可能です (要確認)。

実装

既存のオープンソース実装

EPFL の Computer Graphics and Geometry Laboratory によって開発された実装がオープンソースとして公開されています。

ShapeOp: Open-source C++ Library for Geometry Processing

今回実装するにあたって、クラス構造などを中心に ShapeOp による実装を参考にしました。

使用ライブラリ

以下のライブラリを使用しました。

Eigen (線形システムソルバー *15、ベクトル・行列クラス)
libigl (三次元モデルの読み込み、法線方向の計算)

並列化

C++11 の std::thread を用いてマルチスレッド化を行いました *16。具体的には local solve 部分は制約毎に並列化が可能で、global solve 部分は各座標軸 ( $x, y, z$ ) 毎に並列化が可能です。

制約

今回は布のシミュレーションを実装するために最低限な

Triangle strain 制約
位置制約

の二つを実装しました。布のシミュレーションとしては

Edge strain 制約
Bending 制約
衝突制約

なども実装すると良いと思いますが、今回は扱いません。

実行環境

以下の結果は MacBook Pro (Retina, 13-inch, Mid 2014) で実行しています。CPU は 3 GHz Intel Core i7 です。リアルタイム描画ではなく連番画像を出力する実装になっています。

結果

結果１：異なる解像度

この論文で projective dynamics のために提案された連続体ベースの制約群は、メッシュの解像度の変化や非一様性に対してロバストに動作するのが特徴です。以下の動画では異なるメッシュの解像度でも (皺の詳細度の違いこそあれど) 似た結果が得られていることを確認しています。これは従来 *17 の PBD では実現できなかった性質です。

この動画では全ての例で反復回数を 15 回に統一しています。

以下に計算時間を示します。リアルタイム計算と呼べるのが 15 [ms / frame] 程度までと考える *18 と、概ね 5k DoFs まではリアルタイムで動くといって良さそうです。

#triangles	#dofs	initialize [ms]	local [ms / iteration]	global [ms / iteration]	overall [ms / frame]
64	123	0.096	0.147	0.111	4.011
256	435	0.263	0.191	0.138	5.108
1,024	1,635	0.949	0.306	0.180	7.553
4,096	6,339	4.245	0.704	0.374	16.78
16,384	24,963	28.63	2.309	1.589	60.28
65,536	99,075	256.7	9.619	9.344	291.8

結果２：異なる反復回数

Projective dynamics の最大の特徴は、反復回数を増やせば増やすほど正しい *19 解に収束していくことです。以下の動画では反復回数をだんだんと増やしたときに挙動が収束していくことを確認しています。これも従来 *20 の PBD では実現できなかった性質です。

この動画では全ての例でメッシュ解像度を #triangles = 16,384 に統一しています。計算時間はほぼ反復回数に比例しています。この例では 10 回程度反復すれば十分な印象です。解像度を高くしたり、硬い材質を表現するために制約の重みを大きくしたりすると、より多くの反復が必要になると思います。

Projective Dynamics は PBD に取って代わるものになるか？

Projective dynamics の論文を読む限り PBD よりもずっと良さそうに見えますが、将来どちらが市民権を獲得することになるかは今のところ判断できないというのが結論です。理由は以下の 4 点です。

理由１：2014 年以降に発表された PBD の拡張手法が結構良さそう

Projective dynamics の論文が投稿された 2014 年 1 月の段階では、PBD には

連続体ベースの制約が扱えないため、結果がメッシュに依存してしまう
反復回数に依存して結果が変わってしまう

という欠点がありました。今回の論文ではこれらの欠点を解消することに成功しています。

しかしその後、PBD で連続体ベースの制約が扱えるようになった [Muller et al. 2014] (要確認) り、反復回数に依存して結果が変わってしまう問題を解消する (要確認) 手法 XPBD が提案されたり [Macklin et al. 2016] してきています。これらによって projective dynamics を採用する利点は小さくなっているように思えます。

理由２：Projective dynamics は PBD に比べ計算時間がかかる

実は projective dynamics の local solve は PBD の反復計算とほぼ同等の処理を行っています。したがってこの部分の計算コストはほぼ同等と考えられます。

一方で projective dynamics には global solve の処理が存在します。この処理によって反復回数に依存して結果が変わってしまう問題を解消できる反面、PBD よりも計算コストが上がってしまっています。あくまで目安ですが、今回の実装ではおよそ 1.5 倍から 2 倍程度、global solve によって全体の計算コストが上昇したと考えられます。

Local solve は GPU を駆使することで格段に速くなる余地がありますが、global solve はこれ以上の並列化は困難です。したがって、どうしても projective dynamics は PBD よりも大幅に計算時間がかかってしまうことになります。

追記 (2017/02/09)：Global solve を GPU で並列化する論文が Wang [2015] によって提案されていました。ご指摘ありがとうございます。この論文では global solve にあたる線形方程式の計算を GPU 上で Jacobi 法を使って解く方法を説明しており、さらに Chebyshev 準反復法と呼ばれる手法を組み合わせることで projective dynamics の大幅な高速化を行っています。

Huamin Wang. 2015. A chebyshev semi-iterative approach for accelerating projective and position-based dynamics. ACM Trans. Graph. 34, 6, Article 246 (October 2015), 9 pages. DOI: http://dx.doi.org/10.1145/2816795.2818063

理由３：Projective dynamics は PBD に比べ柔軟性に欠ける

Projective dynamics では global solve の係数行列を事前に分解しておくことで実行時には高速に方程式を解くことができます。しかし、制約が変わる場合はこの計算コストの高い行列分解を再計算する必要が生じてしまうことから、PBD に比べ柔軟性に欠けるという問題があります。

例えばパーティクルベースの流体シミュレーションでは、粒子間の制約が (ほぼ) 毎ステップ、動的に変わっていきます。柔軟性に欠ける projective dynamics では、毎ステップ行列分解をするのを避けるために、matrix-free CG 法を用いて枠組みに変更を加えた上で流体シミュレーションを実現する必要があります [Weiler et al. 2016]。一方で PBD では行列分解を必要としないため、ストレートフォワードに流体シミュレーションを実現することができます [Macklin and Muller 2013]。

理由４：Projective dynamics も 2014 年以降だんだんと進化してきている

PBD だけでなく、projective dynamics もまた 2014 年以降少しずつ拡張手法が提案されてきています。様々な材質の超弾性体 *21 をシミュレーションすることができるようになったり [Narain et al. 2016; Liu et al. 2016]、ハード制約 *22 が扱えるようになったり [Narain et al. 2016] してきています。

(一応) 結論

Projective dynamics は計算コストを小さく保ったままより物理的に正確な表現を実現する方向で発展していることもあり、映像制作にはかなり向いている印象です。一方で PBD はその計算スピード・柔軟性・近年の拡張手法の存在から、ゲームや VR などのインタラクティブコンテンツでは依然として選ばれ続ける気がします。

最後に

本記事に誤りや分かり難い点などを見つけた際には、些細な点でも構いませんので、ご連絡いただけると嬉しいです。

References

Sofien Bouaziz, Sebastian Martin, Tiantian Liu, Ladislav Kavan, and Mark Pauly. 2014. Projective dynamics: fusing constraint projections for fast simulation. ACM Trans. Graph. 33, 4, Article 154 (July 2014), 11 pages. DOI: http://dx.doi.org/10.1145/2601097.2601116
Isaac Chao, Ulrich Pinkall, Patrick Sanan, and Peter Schröder. 2010. A simple geometric model for elastic deformations. ACM Trans. Graph. 29, 4, Article 38 (July 2010), 6 pages. DOI: http://dx.doi.org/10.1145/1778765.1778775
Yuki Koyama, Kenshi Takayama, Nobuyuki Umetani, and Takeo Igarashi. 2012. Real-time example-based elastic deformation. In Proc. SCA '12. 19-24. DOI: http://dx.doi.org/10.2312/SCA/SCA12/019-024
Tiantian Liu, Adam W. Bargteil, James F. O'Brien, and Ladislav Kavan. 2013. Fast simulation of mass-spring systems. ACM Trans. Graph. 32, 6, Article 214 (November 2013), 7 pages. DOI: http://dx.doi.org/10.1145/2508363.2508406
Tiantian Liu, Sofien Bouaziz, Ladislav Kavan. 2016. Towards real-time simulation of hyperelastic materials. arXiv:1604.07378. URL: http://arxiv.org/abs/1604.07378
Miles Macklin and Matthias Müller. 2013. Position based fluids. ACM Trans. Graph. 32, 4, Article 104 (July 2013), 12 pages. DOI: http://dx.doi.org/10.1145/2461912.2461984
Miles Macklin, Matthias Müller, and Nuttapong Chentanez. 2016. XPBD: position-based simulation of compliant constrained dynamics. In Proc. MIG '16. 49-54. DOI: https://doi.org/10.1145/2994258.2994272
Sebastian Martin, Bernhard Thomaszewski, Eitan Grinspun, and Markus Gross. 2011. Example-based elastic materials. ACM Trans. Graph. 30, 4, Article 72 (July 2011), 8 pages. DOI: http://dx.doi.org/10.1145/2010324.1964967
Matthias Müller, Nuttapong Chentanez, Tae-Yong Kim, and Miles Macklin. 2015. Strain based dynamics. In Proc. SCA '14. 149-157. DOI: http://dx.doi.org/10.2312/sca.20141133
Matthias Müller, Bruno Heidelberger, Marcus Hennix, and John Ratcliff. 2007. Position based dynamics. J. Vis. Comun. Image Represent. 18, 2 (April 2007), 109-118. DOI: http://dx.doi.org/10.1016/j.jvcir.2007.01.005
Rahul Narain, Matthew Overby, and George E. Brown. 2016. ADMM ⊇ projective dynamics: fast simulation of general constitutive models. In Proc. SCA '16. 21-28. DOI: http://dx.doi.org/10.2312/sca.20161219
Huamin Wang, James O'Brien, and Ravi Ramamoorthi. 2010. Multi-resolution isotropic strain limiting. ACM Trans. Graph. 29, 6, Article 156 (December 2010), 10 pages. DOI: http://dx.doi.org/10.1145/1882261.1866182
Marcel Weiler, Dan Koschier, and Jan Bender. 2016. Projective fluids. In Proc. MIG '16. 79-84. DOI: https://doi.org/10.1145/2994258.2994282